二项期权定价模型

　　二项期权定价模型又称为二项式模型(Binomial Model)或二叉树法(Binomial tree)，是指于1979年提出的一种对离散时间的期权定价的简化模型，主要用于计算美式期权的价值。

　　二项期权定价模型由约翰·考克斯(John Carrington Cox)、斯蒂芬·罗斯（Stephen A.Ross）、马克·鲁宾斯坦（Mark Rubinstein）和威廉·夏普(William F.Sharpe)等人提出。

　　基本假设：

　　（1）标的资产的未来价格只有上涨或下跌两种情况；

　　（2）标的资产的未来价格上涨或下跌的报酬率已知，且投资人能利用现货市场及资金借贷市场；

　　（3）建立与期权报酬变动完全相同的对冲资产组合；

　　（4）无摩擦市场，即无交易成本、税负等，且证券可以无限分割；

　　（5）借贷利率均相等，皆为无风险利率；

　　（6）每一期借贷利率（r）、上行乘数（u）和下行乘数（d）均已知，且存在如下关系，u>1且d<1，u>R>d，否则会出现套利机会。

　　①单期二叉树模型（与复制原理和风险中性原理的计算方式相同）

　　以风险中性原理为例：

　　将上行概率与下行概率公式带入（1）得

　　②两期二叉树模型

　　如果把单期二叉树模型的到期时间分割成两部分，就形成了两期二叉树模型。由单期模型向两期模型的扩展，不过是单期模型的两次应用。

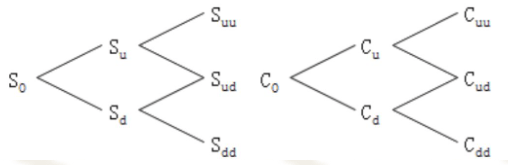
　　注：如果期数比较多，不常用复制原理，多用风险中性原理，各期的是概率不变。

　　③多期二叉树模型

　　从原理上看，与两期模型一样，从后向前逐级推进，期数增加以后带来的主要问题是股价上升与下降的百分比如何确定问题。期数增加以后，要调整价格变化的升降幅度，以保证年收益率的标准差不变。把年收益率标准差和升降百分比联系起来的公式是：

　　其中，e=自然对数，σ=标的资产连续复利收益率的标准差（未来收益率的标准差往往无法确定，根据历史数据来计算），t=以年表示的时间长度（每一期长度用年表示）。

　　1973年，布莱克和休尔斯(Blackand Scholes)提出了布莱克-休尔斯期权定价公式，对标的资产的价格服从正态分布的期权进行定价。随后，罗斯开始研究标的资产的价格服从非正态分布的期权定价理论。1976年，约翰·考克斯(John Carrington Cox)、斯蒂芬·罗斯(Stephen A.Ross)在《金融经济学杂志》上发表论文“基于另类随机过程的期权定价”，提出了风险中性定价理论。

　　1979年，约翰·考克斯(John Carrington Cox)、斯蒂芬·罗斯(Stephen A.Ross)、马克·鲁宾斯坦（Mark Rubinstein）在《金融经济学杂志》上发表论文“期权定价：一种简单的方法”，该文提出了一种简单的对离散时间的期权的定价方法，被称为Cox-Ross-Rubinstein二项式期权定价模型。

　　二项式期权定价模型和布莱克-休尔斯期权定价模型，是两种相互补充的方法。二项式期权定价模型推导比较简单，更适合说明期权定价的基本概念。二项式期权定价模型建立在一个基本假设基础上，即在给定的时间间隔内，证券的价格运动有两个可能的方向：上涨或者下跌。虽然这一假设非常简单，但由于可以把一个给定的时间段细分为更小的时间单位，因而二项式期权定价模型适用于处理更为复杂的期权。

　　随着要考虑的价格变动数目的增加，二项式期权定价模型的分布函数就越来越趋向于正态分布，二项式期权定价模型和布莱克-休尔斯期权定价模型相一致。二项式期权定价模型的优点，是简化了期权定价的计算并增加了直观性，因此现在已成为全世界各大证券交易所的主要定价标准之一。

　　一般来说，二项期权定价模型的基本假设是在每一时期股价的变动方向只有两个，即上升或下降。BOPM的定价依据是在期权在第一次买进时，能建立起一个零风险套头交易，或者说可以使用一个证券组合来模拟期权的价值，该证券组合在没有套利机会时应等于买权的价格；反之，如果存在套利机会，投资者则可以买两种产品种价格便宜者，卖出价格较高者，从而获得无风险收益，当然这种套利机会只会在极短的时间里存在。这一证券组合的主要功能是给出了买权的定价方法。与期货不同的是，期货的套头交易一旦建立就不用改变，而期权的套头交易则需不断调整，直至期权到期。