历史波动率

　　历史波动率是指资产在过去一段时间内所表现出的波动率，它是通过统计方法，利用资产历史价格数据计算而得，也可以称其为已实现波动率，是确定性的。历史波动率非常重要，它的大小不仅体现了金融资产在统计期内的波动状况，更是分析和预测其他几类波动率的基础。

　　历史波动率的估计思路一般是根据资产价格时间序列数据，计算出相应的波动率数据，然后运用统计推断方法估算回报率的标准差，从而得到历史波动率的估计值。

资产价格时间序列数据处理

　　在处理资产价格时间序列数据时，一般有两个方法：百分比价格变动法和对数价格变动法。

　　百分比价格变动法(即价格的环比增长速度)计算公式为：

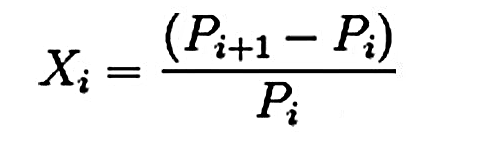
　　其中，Xi是资产的百分比收益，Pi是基期资产的价格，Pi+1是报告期资产的价格。

　　对数价格变动法计算公式为：

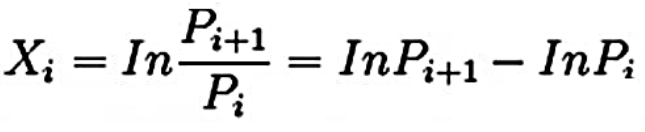
　　其中，Xi是资产的对数收益，Pi是基期资产的价格，Pi+1是报告期资产的价格。

　　值得注意的是，上述两个公式的假定不一样，百分比收益公式假定有固定的不连续间隔价格变化，而对数收益公式假定价格是连续的变化。在Black-Scholes模型中，假定价格变动是连续的。所以，在研究估计波动率时一般采用对数收益公式。

度量波动率常见方法

　　度量波动率的方法有很多，比较常见的是标准方差波动率、Parkinson估计量、Garman-Klass估计量和Yang-Zhang估计量。

　　波动率的标准定义是方差的平方根，具体计算为针对资产的对数收益求其平均数，然后根据下面公式得到历史波动率的估计值。

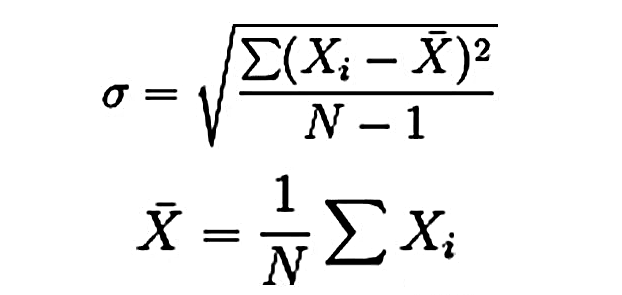
　　这里，N是观察值的数量，σ代表对数收益的平均离差，即标准差。若将日、周等标准差转化为年标准差，需要乘以以年为单位的频数长度的平方根。如美国期权市场一年有252个工作日，Xi为日变量，则年波动率为：

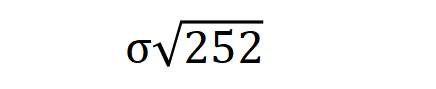
　　标准方差波动率没有考虑一些具体情况，如股息的支付(或者拆股)，仅是历史波动率粗糙的表征，但标准方差波动率是各种调整方法的基础，Parkinson估计量、Garman-Klass估计量和Yang-Zhang估计量等估计方法都是在标准方差波动率基础上进行了一定的改进。

　　Parkinson(1980)估计量采用了交易时段最高价和最低价两个价格数据，利用极差进行估计，该估计量只需要较少的时间周期就可以收敛于真实波动率。该估计量可以使价格波动区间在一定假设下比基于收盘价的估计量更能有效地估计回报波动率。

　　Parkinson(1980)估计量提供了一个对日最高与最低价格经验性质的探究性分析，建立了一个基于最高价和最低价时间序列预测模型，对未来价格波动区间的量化分析提供了重要的参考。

　　Garman-Klass（1980）利用了交易时段最高价、最低价和收盘价三个价格数据进行估计，该估计量通过将估计量除以调整因子来纠正存在的偏差，以便得到方差的无偏估计。但Garman-Klass（1980）估计量无法解决价格序列中存在跳空开盘的情况。

　　Yang-Zhang（2000）推导出了适用于价格跳空开盘的估计量，本质上是各种估计量的加权平均。

　　上述讨论的几种波动率估计量，每类估计量都克服了上类估计量的不足，因此每次更迭都比上一次更优。但值得注意的是，在仿真和实际环境下进行测试表明，没有任何迹象显示哪一个估计量是最好的，因为所有的度量方法都包含一定的信息量。

　　如果Parkinson波动率是50%，而标准方差波动率只有20%，至少可以认为真实波动率绝大部分是由较大的日内极差造成的，在决定对冲策略时，这些信息是很有用的。

　　1、风险评估：

　　历史波动率可以帮助投资者了解资产价格的波动情况，从而评估投资风险。

　　如果历史波动率较高，说明资产价格波动较大，投资者面临的风险也相应较大。

　　2、资产配置：

　　历史波动率可以帮助投资者在资产配置方面做出更明智的决策。

　　例如，投资者可以根据不同资产的历史波动率来调整其投资组合的配置比例，以实现风险和收益的平衡。

　　3、预测未来波动：

　　虽然历史波动率并不能直接预测未来的波动情况，但通过对历史数据的分析，投资者可以获得对未来波动率趋势的一些启示。

　　例如，如果历史数据显示某一资产的波动率长期处于上升趋势，那么未来该资产的波动率可能继续上升。