布莱克-斯科尔斯期权定价模型
布莱克-斯科尔斯期权定价模型(简称BS模型)是理财学中最复杂的公式之一,其证明和推导过程涉及复杂的数学问题,但使用起来并不困难。该公式有非常重要的意义,它对理财学具有广泛的影响,是近代理财学不可缺少的内容。该模型具有实用性,被期权交易者广泛使用,实际的期权价格与模型计算得到的价格非常接近。
布莱克-斯科尔斯模型的假设
(1)在期权寿命期内,期权标的股票不发股利,也不做其他分配;
(2)股票或期权的买卖没有交易成本;
(3)短期的无风险利率是已知的,并且在期权寿命期内保持不变;
(4)任何证券购买者都能以短期的无风险利率借得任何数量的资金;
(5)允许卖空,卖空者将立即得到所卖空股票当天价格的资金;
(6)看涨期权只能在到期日执行;
(7)券续发生的,股票价格随机游走。
布莱克-斯科尔斯模型
布莱克-斯科尔斯模型的公式如下:
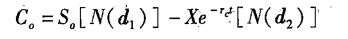
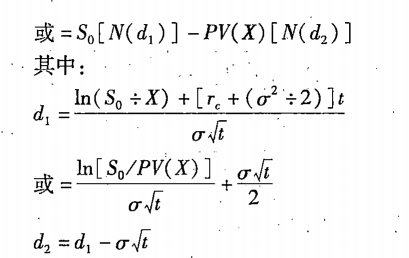
其中:C0表示看涨期权的当前价值;S0表示标的股票的当前价格;N(d)表示标准正态分布中离差小于d的概率;X表示期权的执行价格;e表示自然对数的底数,约等于2.7183;rC表示连续复利的年度无风险利率;t表示期权到期日前的时间(年);ln(S0÷X)表示S0÷X的自然对数;σ2 表示连续复利的以年计的股票报酬率的方差。
如果直观(不准确)地解释,它的第一项是最终股票价格的期望现值,第二项是期权执行价格的期望现值,两者之差是期权的价值。
公式的第一项是当前股价和概率N(d1)的乘积。股价越高,第一项的数值越大,期权C0。价值越大。公式的第二项是执行价格的现值Xe–rct 和概率N(d2)的乘积。Xe–rct 是按连续复利计算的执行价格X的现值,也可以写成PV(X)。执行价格越高,第二项的数值越大,期权的价值C0,越小。
概率N(d1)和N(d2)可以大致看成看涨期权到期时处于实值状态的风险调整概率。当前股价和N(d1)的乘积是股价的期望现值,执行价格的现值与N(d2)的乘积是执行价格的期望现值。
在股价上升时,d和dz都会上升,N(d1)和N(d2)也都会上升,股票价格越是高出执行价格,期权越有可能被执行。简而言之,N(d1)和N(d2)接近1时,期权肯定被执行,此时期权价值等于S0-Xe–rct 。前一项是期权持有者拥有的对当前价格为S0的要求权,后一项是期权持有者的期权执行价格的现值。反过来看,假定N(d1)和N(d2)接近0时,意味着期权几乎肯定不被执行,看涨期权的价值C0接近0。如果N(d1)和N(d2)等于0~1之间的数值,看涨期权的价值是其潜在收入的现值。
布莱克-斯科尔斯模型参数的估计
布莱克-斯科尔斯模型有5个参数。其中,现行股票价格和执行价格容易取得。至到期日的剩余年限计算,一般按自然日(1年365天或为简便用360天)计算,易于确定。但无风险利率和股票报酬率的标准差,难以估计。
(1)无风险利率的估计。无风险利率应当用无违约风险的固定证券收益来估计,例如政府债券的利率。政府债券的到期时间不等,其利率也不同。应选择与期权到期日相同的政府债券利率,例如:期权还有3个月到期,就应选择3个月到期的政府债券利率。如果没有相同时间的,应选择时间最接近的政府债券利率。
这里所说的政府债券利率是指其市场利率,而不是票面利率。政府债券的市场利率是根据市场价格计算的到期报酬率。再有,模型中的无风险利率是指按连续复利计算的利率,而不是常见的年复利。由于布莱克-斯科尔斯模型假设套期保值率是连续变化的,
因此,利率要使用连续复利。连续复利假定利息是连续支付的,利息支付的频率比每秒1次还要频繁。
如果用F表示终值,P表示现值,rC表示连续复利率,t表示时间(年),则:
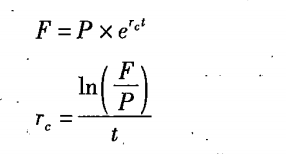
其中:In表示求自然对数。
自然对数的值,很容易在具有函数功能的计算器上计算求得,或者利用“自然对数表”查找,也可以利用Excel的LN函数功能求得。e为连续复利的终值系数,可利用“连续复利终值系数表”查找。
严格说来,期权估值中使用的利率都应当是连续复利,包括二叉树模型和BS型。即使在资本预算中,使用的折现率也应当是连续复利率,因为全年收人和支出总是陆续发生的,只有连续复利率才能准确完成终值和现值的折算。在使用计算机运算时,采用连续复利通常没有什么困难,但是手工计算则比较麻烦。为了简便,手工计算时往往使用分期复利作为连续复利的近似替代。由于期权价值对于利率的变化并不敏感,因此这种简化通常是可以接受的。
使用分期复利时也有两种选择:①按有效年利率折算。例如,有效年利率为4%,则等价的半年利率为√(1+4%)-1=1.98%。按报价利率折算。例如,报价利率为4%,则半年利率为4%÷2=2%。
(2)酬率标准差的估计。
股票报酬率的标准差可以使用历史报酬率来估计。计算连续复利标准差的公式与年复利相同:
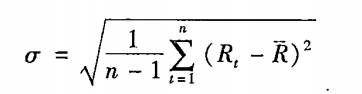
其中:Rt指报酬率的连续复利值。
连续复利的报酬率公式与分期复利报酬率不同:
分期复利的股票报酬率:
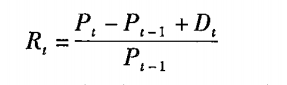
连续复利的股票报酬率:
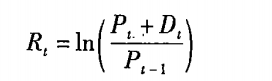
其中:Rt表示股票在t时期的报酬率;Pt表示t期的价格;Pt-1表示t-1期的价格;Dt表示t的股利。
在期权估值中,严格说来应当使用连续复利报酬率的标准差。有时为了简化,也可以使用分期复利报酬率的标准差作为替代。
看跌期权估值
前面的讨论主要针对看涨期权,那么,如何对看跌期权估值呢?在套利驱动的均衡状态下,看涨期权价格、看跌期权价格和股票价格之间存在一定的依存关系。对于欧式期权,假定看涨期权和看跌期权有相同的执行价格和到期日,则下述等式成立:
看涨期权价格C - 看跌期权价格P = 标的资产价格S - 执行价格现值PV ( X )
这种关系被称为看涨期权-看跌期权平价定理(关系)。利用该定理,已知等式中的4个数据中的3个,就可以求出另外1个。
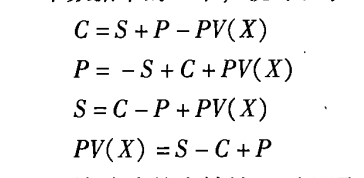
派发股利的期权定价
布莱克-斯科尔斯期权定价模型假设在期权寿命期内买方期权标的股票不发放股利,那么在标的股票派发股利的情况下应如何对期权估值呢?股利的现值是股票价值的一部分,但是只有股东可以享有该收益,期权持有人不能享有。因此,在期权估值时要从股价中扣除期权到期日前所派发的全部股利的现值。也就是说,把所有到期日前预期发放的未来股利视同已经发放,将这些股利的现值从现行股票价格中扣除。此时,模型建立在调整后的股票价格而不是实际价格基础上。
考虑派发股利的期权定价公式如下:
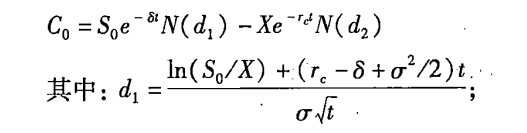
σ表示标的股票的年股利报酬率(假设股利连续支付,而不是离散分期支付);如果标的股票的年股利报酬率σ为0,则与前面介绍的布莱克-斯科尔斯模型相同。
附件列表
免责声明:
- • 会计网百科的词条系由网友创建、编辑和维护,如您发现会计网百科词条内容不准确或不完善,欢迎您联系网站管理员开通编辑权限,前往词条编辑页共同参与该词条内容的编辑和修正;如您发现词条内容涉嫌侵权,请通过 tougao@kuaiji.com 与我们联系,我们将按照相关法律规定及时处理。
- • 未经许可,禁止商业网站等复制、抓取会计网百科内容;合理使用者,请注明来源于baike.kuaiji.com。

 沪公网安备
31010902002985号
沪公网安备
31010902002985号