投入产出表

　　投入产出表，即产品部门×产品部门表，由三个象限组成。第一象限是行列名称相同、次序相同的n×n个产品部门的方阵，主栏为中间投入，宾栏为中间使用，反映国民经济各产品部门之间的技术经济联系。行向看，反映第i产品部门生产并提供给第j产品部门使用的货物和服务价值量；列向看，反映第j产品部门在生产过程中消耗第i产品部门生产的货物和服务价值量。

　　第二象限是第一象限在水平方向上的延伸，其主栏与第一象限的主栏相同，也是n个产品部门；其宾栏主要由最终消费支出、资本形成总额、出口等最终使用项目组成，主要反映各产品部门生产并用于各种最终使用的货物和服务价值量及其构成。第三象限是第一象限在垂直方向上的延伸，其主栏由劳动者报酬、生产税净额、固定资产折旧、营业盈余等增加值项目组成；宾栏与第一象限的宾栏相同，也是n个产品部门，反映各产品部门增加值的构成情况。

　　供给表、使用表、投入产出表之间存在着密切的联系。在一定的假设下，可以通过供给表和使用表推导出投入产出表，也可以通过供给表和投入产出表推导出使用表。另外，供给表和使用表还存在如下平衡关系：

　　1、供给表中按购买者价格计算的各产品部门总供给＝使用表中按购买者价格计算的各产品部门总使用

　　2、供给表中各产业部门总产出＝使用表中各产业部门总投入

　　投入产出分析包括投入产出表数据分析和投入产出模型分析两类。利用投入产出表数据可以直接进行产业结构、最终使用结构等分析。投入产出模型分析需要首先根据投入产出表平衡关系建立模型，再利用模型进行各种定量分析。这里主要介绍投入产出模型分析。

　　进行投入产出模型分析，首先要了解以下主要系数和矩阵。

相关系数和计算公式

　　1.直接消耗系数

　　直接消耗系数，也称投入系数，记为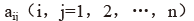，它是指生产一个单位某种产品对另一种产品的消耗量。计算方法为：

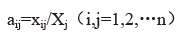
　　式中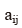，为直接消耗系数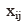，为j产品部门生产中消耗i部门产品的价值量，为各部门总投入（总产出）。

　　将各产品部门的直接消耗系数用表的形式表现就是直接消耗系数表或直接消耗系数矩阵，通常用字母A表示。

　　2.完全消耗系数

　　对完全消耗的理解可以小汽车生产中对电的需求为例。生产一辆小汽车需要直接消耗其他部门的产品，如电力、钢铁、橡胶、电子产品等等。而电力的生产需要煤，橡胶的生产需要农业，钢铁的生产需要铁矿石，钢铁与铁矿石的生产还需要电力。小汽车对电力的直接消耗加上所有的间接消耗就是小汽车对电力的完全消耗。

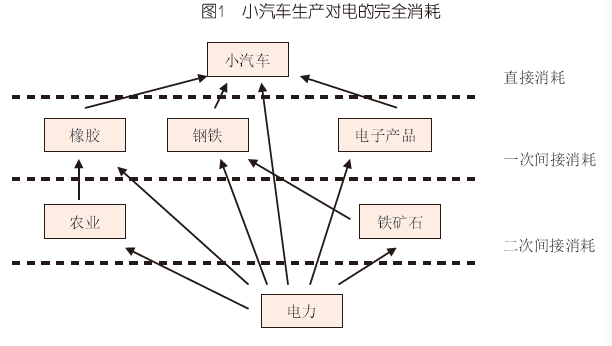
　　完全消耗系数，通常记为，是指某产品j生产单位最终产品量对另一产品i的完全消耗量，即第j产品部门每提供一个单位最终使用时，对第i产品部门货物或服务的直接消耗和间接消耗之和。计算方法为：

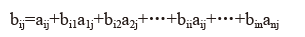
　　利用直接消耗系数矩阵A计算完全消耗系数矩阵B的公式为：

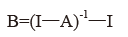
　　式中的I为单位矩阵。

　　在完全消耗系数矩阵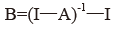中，矩阵称为列昂惕夫逆矩阵，记为B。其元素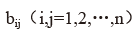称为列昂惕夫逆系数，它表明第j部门增加一个单位最终使用时，对第i产品部门的完全需要量。

投入产出模型

　　在定义上述系数和矩阵的基础上，可以建立投入产出行模型和列模型。

　　1.行模型

　　行模型是基于投入产出表行的平衡关系建立的。行模型揭示了国民经济各部门生产的货物和服务的使用去向，可以用来测算为了满足某些部门的最终需求，每个部门必须要达到的产出水平。

　　行模型为：中间使用+最终使用=总产出用矩阵表示：AX+Y=X

　　可变换为：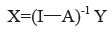

　　2.列模型

　　列模型主要是基于投入产出表列的平衡关系建立的。列模型揭示了国民经济各部门生产过程中发生的各种投入，可以用来研究国民经济各部门生产货物和服务的价值形成问题。

　　列模型为：中间投入+初始投入（增加值）=总投入用矩阵表示：XH+V=X

　　可变换为：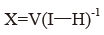

　　其中，H为直接分配系数。类比于列昂惕夫逆系数，也可以定义为完全分配系数。

　　基于上述投入产出行模型和列模型，结合其他经济学理论和假定，投入产出表可作为重要的经济分析工具，应用于经济结构分析、能源环境研究、区域经济一体化与协调发展、全球价值链等诸多领域，能够为制定有关政策、加强宏观经济管理提供有力的数据支撑。

　　下面的应用实例，测算的是基于2017年投入产出表中数据，第三产业增加值增长1%对经济的影响。

　　测算时首先利用列模型测算各部门总产出，再根据最终使用、增加值等指标与总产出的关系，计算出对最终使用构成项及劳动者报酬的影响，计算结果如下：

　　由表2可见，第三产业增加值增长1%，居民消费增长0.54%，最终消费增长0.61%，劳动者报酬增长0.53%。