经济订货量
经济订货量是指能够使成本最小化的每次订货量,由于购置成本和每次订货数量无关,决策中不需要考虑,经济订货量实际是能够让批量相关成本(持有成本+订货成本)最小的每次订货数量。
如果每次订购的数量过多,则大量暂时用不完的存货闲置堆积,带来过高的持有成本。如果每次订购的数量过少,则需要频繁订货,带来过高的订货成本。因此,设置最佳的订购数量,需要权衡持有成本和订货成本两项成本。可以证明,当持有成本和订货成本相等的时候,批量相关成本能够实现最小化,这一原理称为“两项相等和最小”。
经济订货量的基本模型
构建经济订货量基本模型需要的假设条件有:
(1)企业能够及时补充存货,即需要订货时便可立即取得存货。
(2)货物能集中到货,而不是陆续入库。
(3)不允许缺货,即无缺货成本,TC为0,这是因为良好的存货管理本来就不应该出现缺货成本。
(4)货物的年需求量稳定,并且能够预测,即D为已知常量。
(5)存货单价不变,即U为已知常量。
(6)企业现金充足,不会因现金短缺而影响进货。
(7)所需存货市场供应充足,不会因买不到需要的存货而影响其他方面。
在上列假设条件下,存货总成本的公式可以写成:
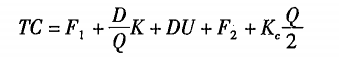
当K、D、U、F2、KC为常数量时,TC的大小取决于Q。为了求出TC的最小值,对其进行求导演算,可得出下列公式:
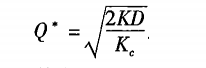
其中:K表示一次订货变动成本;D示存货年需求量;KC表示单位储存变动成本。
这一公式称为经济订货量基本模型,求出的每次订货批量,可使TC达到最小值。
这个基本模型还可以演变为其他形式:
每年最佳订货次数公式:
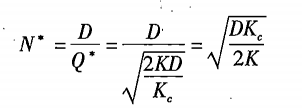
与批量有关的存货总成本公式:
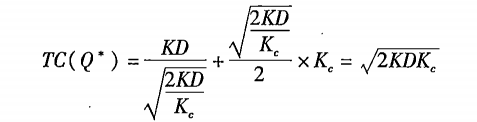
最佳订货周期公式:
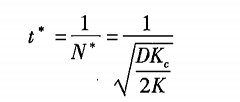
经济订货量占用资金:
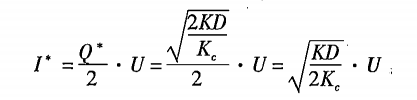
经济订货量基本模型的扩展
经济订货量的基本模型是在前述各假设条件下建立的,但现实生活中能够满足这些假设条件的情况十分罕见。为使模型更接近于实际情况,具有较高的可用性,需逐一放宽假设,同时改进模型。
1.订货提前期
一般情况下,企业的存货不能做到随用随时补充,因此不能等存货用光后再去订货,而需要在没有用完时提前订货。在提前订货的情况下,企业再次发出订货单时,尚有存货的库存量,称为再订货点,用R来表示。在不存在保险储备的情况下,它的数量等于平均交货时间(L)和每日平均需求量(d)的乘积:
R=Ld
2.存货陆续供应和使用
在建立基本模型时,是假设存货一次全部人库,故存货增加时存量变化为一条垂直的直线。事实上,各批存货可能陆续入库,使存量陆续增加。尤其是产成品人库和在产品转移,几乎总是陆续供应和陆续耗用的。在这种情况下,需要对基本模型做一些修改。
3.保险储备
以前讨论假定存货的供需稳定且确知,即每日需求量不变,交货时间也固定不变。实际上,每日需求量可能变化,交货时间也可能变化。按照某一订货批量(如经济订货批量)和再订货点发出订单后,如果需求增大或送货延迟,就会发生缺货或供货中断。为防止由此造成的损失,就需要多储备一些存货以备应急之需,这称为保险储备(安全存量)。这些存货在正常情况下不动用,只有当存货过量使用或送货延迟时才动用。
再订货点R=平均交货时间×每日平均需求量+保险储备
建立保险储备,固然可以使企业避免缺货或供应中断造成的损失,但存货平均储备量加大却会使储备成本升高。研究保险储备的目的,就是要找出合理的保险储备量,使缺货或供应中断损失和储存成本之和最小。方法上可先计算出各不同保险储备量的总成本,然后再对总成本进行比较,选定其中最低的。
如果设与此有关的总成本为TC(S、B),缺货成本为CS,保险储备成本为CB则:
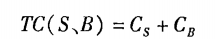
设单位缺货成本为KU;,一次订货缺货量为S,年订货次数为N,保险储备量为B,单位储存变动成本为KC,则:
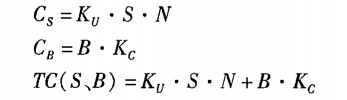
现实中,缺货量S具有概率性,其概率可根据历史经验估计得出;保险储备量B可选择而定。
附件列表
免责声明:
- • 会计网百科的词条系由网友创建、编辑和维护,如您发现会计网百科词条内容不准确或不完善,欢迎您联系网站管理员开通编辑权限,前往词条编辑页共同参与该词条内容的编辑和修正;如您发现词条内容涉嫌侵权,请通过 tougao@kuaiji.com 与我们联系,我们将按照相关法律规定及时处理。
- • 未经许可,禁止商业网站等复制、抓取会计网百科内容;合理使用者,请注明来源于baike.kuaiji.com。

 沪公网安备
31010902002985号
沪公网安备
31010902002985号