平均指标

　　平均指标是反映总体各单位某一数量标志一般水平的综合指标，如职工的平均工资、平均年龄。平均指标的特点是把同质总体内某一数量标志的差异抽象化了，是总体各单位标志值的代表值。利用平均指标可以反映总体分布的集中趋势，同时由于该指标消除了总体范围大小的影响，因此，可以对同类现象在不同单位、不同地区间进行比较研究，在实际工作中应用广泛。

　　（1）可以反映总体各单位变量分布的集中趋势，用来作为评判事物的标准和依据。

　　（2）可以用来比较同类现象在不同单位的发展水平，以说明生产水平、经济效益或工作质量的差距。

　　（3）用来比较同一单位的同类指标在不同时期的发展状况。

　　（4）可用来分析现象之间的依存关系。在统计估计推断中，常用部分单位的平均数去推断总体平均数，或者根据总体平均数来推断总体标志总量。

　　平均指标按计算方法不同分为算术平均数、调和平均数、几何平均数、中位数和众数等几种主要形式。

　　①算术平均数是统计中最基本、最常用的一种平均数。它的基本计算形式是用总体标志总量除以总体单位总数。

　　在实际工作中，根据未分组资料计算平均指标一般采用简单算术平均数的方法，即将总体各单位标志值简单相加除以总体单位总数。用公式表示：

　　式中xi为总体各单位标志值（i=1，2，3，…n），n为总体单位数。

　　根据分组资料计算平均指标就需要用加权算术平均数的方法，即首先计算出各组的总量指标，然后加总计算出总体总量指标，再除以总体单位总数。用公式表示：

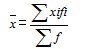
　　式中，xi代表各组的标志值（i=1，2，3，…n），fi代表各组的次数，即权数。

　　②调和平均数是利用标志值倒数计算的平均数，所以也称倒数平均数。在实际工作中，经常会遇到只有各组标志总量和各单位标志值，缺少总体单位数的情况，这时就必须采用调和平均数的方法计算平均指标。

　　简单调和平均数的计算公式：

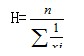
　　加权调和平均数实际上是加权算术平均数的变形。当知道各组的标志总量（xf），而不知道各组的次数(f)时，可以设m=xf，则f=m/x，代入加权算术平均数的计算公式，即：

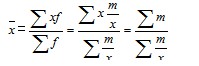
　　由此得到加权调和平均数的计算公式：

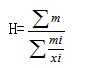
　　其中，mi表示各组的标志总量，在这里作为权数。在具体应用时，如果掌握各单位标志值和相应的次数资料，就采用加权算术平均数公式；如果掌握各单位标志值和各组的标志总量，就采用加权调和平均数公式。

　　③几何平均数是用n个变量值的连乘积开n次方计算的平均数，它适合于计算平均比率和平均速度。其计算公式为：

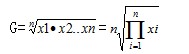
　　式中：xi（i=1，2，3，…n），代表各组的变量值，n为变量值的个数；П为连乘符号。

　　④中位数和众数是将总体中各单位标志值按大小顺序排列，居中间位置的那个标志值就是中位数。如果总体单位数是偶数，则居中间的两个标志值的算术平均数是中位数。由于中位数不受数列中极端值的影响，因此，在一些情况下能更好地反映现象的一般水平。例如居民收入中位数就不受个别极高收入户的影响，比平均收入更具有代表性。

　　总体中出现次数最多的标志值叫众数。利用众数作为社会经济现象一般水平的代表在具体工作中有一定的实用性。例如要了解农贸市场上某种商品的价格水平，只要观察该种商品多数成交价格即可。