C-D生产函数

　　C-D生产函数又称为柯布—道格拉斯生产函数，是由数学家柯布（Cobb，C.W.）和经济学家道格拉斯（Douglas，P.H.）共同创造的生产函数，通过对美国1899—1922年资本和劳动对生产的影响进行测算，得出劳动对产出的贡献高达3/4，创造性地论证了斯密等古典经济学家关于劳动价值论的观点。

　　企业生产函数的讨论具有鲜明的思辨价值，使生产函数这一经济学家的创造大放异彩的，则是美国数学家柯布(C.W.Cobb)和经济学家保罗·道格拉斯(PaulH.Douglas)。他们共同的创造成果，即大名鼎鼎的柯布—道格拉斯生产函数。

　　柯布和道格拉斯借鉴企业生产函数思想，认真研究1899年至1922年美国制造业的生产函数。他们详细统计了美国制造业中以机器和建筑物为主要形式的“固定资本”投入，以原料、半成品和仓库里的成品为主要形式的“流动资本”投入，考察各类固定资本和流动资本投入（即“资本”投入）和制造业雇佣工人数（即“劳动”投入）对总产出的影响。在没有计算机的年代里，他们从这些庞大的数据中得出了如下的函数公式：

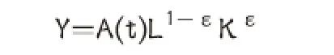
　　这就是柯布—道格拉斯生产函数，是经济学中使用最广泛的一种生产函数形式。其中，Y代表产出，L和K分别代表资本投入和劳动投入，A代表综合技术水平，ε是资本投入与产出的弹性系数。

　　柯布、道格拉斯的研究表明了自己的制造业发展思想，即决定制造业产出水平的主要因素是投入的劳动力数量和各类资本，以及综合技术水平（包括经营管理水平、劳动力素质、引进先进技术等）。在相同的劳动和资本要素投入下，不同技术装备水平的厂商产出水平存有巨大的差异，这是萨缪尔森主张将生产型企业区分为资本密集型企业和劳动密集型企业的原因。在声名远播的柯布—道格拉斯生产函数，并没有提供综合考察并量化计量“综合技术水平”的方法，而是根据产出额扣除劳动、资本贡献后的余值来估算。当时的人们用玩笑的口吻讲，对“综合技术水平”产出贡献的计量，仅仅是“对人类无知的计量”。

　　需要说明的是，创造出柯布—道格拉斯生产函数的柯布、道格拉斯随后吃惊地发现，美国制造业产出的大部分贡献（3/4）应归属于劳动要素。似乎更重视资本要素贡献的两位“发现者”被自己的“发现”吓坏了，竟然表示他们自己千辛万苦得到的结果是值得怀疑的，并强调他们的文章不在于给出结论，而在于演示方法！

　　更需要说明的是，柯布—道格拉斯生产函数的理论缺陷及实际应用一直存有争议。柯布、道格拉斯并没有考虑机器等的技术提升或闲置等情形，也没有考虑劳动时间、劳动者素质变化等复杂情况。机器等资本品并不天然具有生产力，详细计算一定时期一定行业资本、劳动的产出贡献及配置比例后，难以深刻地说明内在原因。正如李嘉图指出的，“维持劳动的资本和投在工具、机器和建筑物上的资本可能结合的比例也是多种多样的”。马克思更是指出，“在不变资本和剩余价值之间，从而在总资本价值（=V+C）和剩余价值之间，没有任何内在的、必然的关系”（《资本论》第3卷）。柯布—道格拉斯生产函数提供了要素、产出之间量化分析的工具，这一工具提供了不变固定资本和产出之间“表面的数量关系”，二者之间可以有多种多样的数量比例，并没有内在的、必然的关系。

　　式中Y是工业总产值，A（t）是综合技术水平，L是投入的劳动力数，K是投入的资本，一般指固定资产净值，α是劳动力产出的弹性系数，β是资本产出的弹性系数，μ表示随机干扰的影响，μ≤1。从这个模型看出，决定工业系统发展水平的主要因素是投入的劳动力数、固定资产和综合技术水平（包括经营管理水平、劳动力素质、引进先进技术等）。

　　根据α和β的组合情况，它有三种类型：

　　①α+β>1，规模报酬递增，表明按照现有技术，用扩大生产规模来增加产出是有利的。

　　②α+β<1，规模报酬递减，表明按照现有技术，用扩大生产规模来增加产出是得不偿失的。

　　③α+β=1，规模报酬不变，表明生产效率并不会随着生产规模的扩大而提高，只有提高技术水平，才会提高经济效益。