几何平均收益率
投资术语
几何平均收益率是将各个单个期间的收益率乘积,然后开n次方。几何平均收益率使用了复利的思想,即考虑了资金的时间价值,也就是说,期初投资1元,第一期末则值(1+R1)元,第二期投资者会将(1+R1)进行再投资,到第二期末价值则为(1+R1)(1+R2)元,……。
几何平均收益率的计算公式
几何平均收益率即计算投资理财产品各期收益率的几何平均值。几何平均收益率的计算公式为:
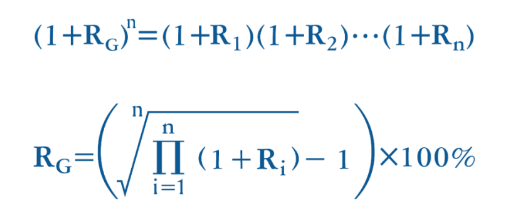
几何平均收益率案例
以例子进行说明:某种股票的市场价格在第1年年初时为100元,到了年底股票价格上涨至200元,但时隔1年,在第2年年末它又跌回到了100元。假定这期间公司没有派发过股息,这样第1年的投资收益率为100%
[R1=(200-100)/100=1=100%],第2年的投资收益率则为-50%
[R2=(100-200)/200=-0.5=-50%]。
实际上,投资者尽管进行了两年的股票投资,但他的实际财富情况并未发生任何变化,其净收益为零。采用几何平均收益率来计算:
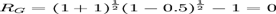
这个计算结果符合实际情况,即两年来平均收益率为零。
几何平均收益率的作用
几何平均收益率,显示在按年进行复利的情况下,平均每年实际赚多少。其运用了复利思想,即考虑了货币的时间价值,能够更准确地反映投资者的真实收益情况。
附件列表
免责声明:
- • 会计网百科的词条系由网友创建、编辑和维护,如您发现会计网百科词条内容不准确或不完善,欢迎您联系网站管理员开通编辑权限,前往词条编辑页共同参与该词条内容的编辑和修正;如您发现词条内容涉嫌侵权,请通过 tougao@kuaiji.com 与我们联系,我们将按照相关法律规定及时处理。
- • 未经许可,禁止商业网站等复制、抓取会计网百科内容;合理使用者,请注明来源于baike.kuaiji.com。

 沪公网安备
31010902002985号
沪公网安备
31010902002985号